I finally gave in and bought a wheelchair last year, when a local store had them on special.
It’s not something I need every day, thankfully. Not even most days. In fact, I’m pretty sure my Mum has borrowed it and used it for my grandmother more times than Mr Happy has used it for me! But thanks to my Dysautonomia and Ehlers-Danlos Syndrome, I suffer from debilitating fatigue, I’m unable to stand for long periods / walk long distances, and I have a propensity for dislocating body parts. So Mr Happy kept prompting that it would be handy for us own one, and after missing out on several events where I could have gone if we’d had one, I gave in.
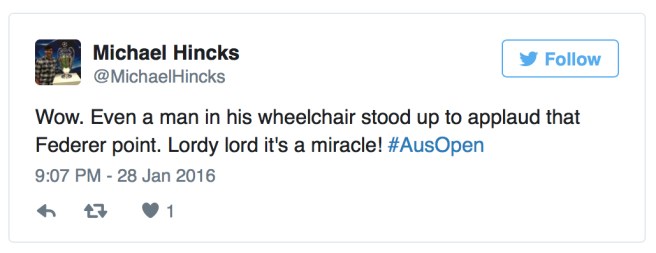
That’s why things like this BuzzFeed post hit me really hard.
Because I know, that could have been me.
That could be me at a sporting event, standing up momentarily to show my enthusiasm and excitement.
But how does that moment of standing prove that I didn’t need the wheelchair?
Do those few seconds in a vertical position mean that I could have managed the long walk from the carpark to the stadium? That I could have easily stood in line for an hour, in the heat, waiting to be seated? That I could have handled climbing all the stairs to my seat?
Of course not.
So how is it a “miracle” if someone stands from a wheelchair?

There’s a common misconception that everyone that uses a wheelchair is paralysed, and therefore should be unable to stand or walk at all.
Why does that misconception matter?
Because a lot of people who use wheelchairs AREN’T paralysed. ¹
And every time they behave in a non-paralysed way (e.g. standing up, walking a few steps), people get offended that they are using a wheelchair.
“Why are you using that thing? If you can walk, why do you need a wheelchair?” they demand, annoyed at the apparent ‘deceit’. They speak as though the wheelchair user has scammed them, tricked them into thinking they were disabled, when in fact, they’re just lazy or looking for sympathy.
But please, allow me to let you in on a secret.
Seriously, lean closer.
It’s pretty shocking.
Nobody WANTS to be in a wheelchair.
Needing one is annoying and humiliating. But there are a giant list of injuries, illnesses and disabilities that they can assist with. So if you see someone using one, and you realise they’re not paralysed, don’t assume they’re using it for fun.
“Are they able to stand / walk?” is not the bar that determines wheelchair use. If that was the correct question, then yes, someone who stood or walked would be a “faker” for using a wheelchair. But the correct indicator of whether someone needs a wheelchair is actually “are they able to stand / walk WITH AN ACCEPTABLE COST?”. If the cost of standing is severe presyncope or fainting, that’s an unacceptable cost. If the cost of walking is severe fatigue, or severe pain, or brain fog so bad they can’t remember what they were actually shopping for – that’s an unacceptable cost.
And if using a wheelchair lessens those unacceptable costs, then they’re not a “faker” for using one. That would be like calling an able-bodied person a “faker” because they use a car to drive the 10km to work. Technically, if they’re able-bodied, they could walk the 10km to work. But the cost (time, fatigue, pain) is likely unacceptable to them. Using a car lessens that cost. Same with wheelchair use.
I was amazed the first time I went clothes shopping using my wheelchair. Usually, an outing like that would wipe me out within an hour: I’d be pale, shaking, exhausted, in an incredible amount of pain, my heart rate would be through the roof, and I’d be in danger of passing out and injuring myself. I’d have to be taken home, and would be bedridden for at least the rest of the day, if not several days while I recovered. But the first time I went shopping in my wheelchair…I was able to stay out all day. ALL! DAY! I finished the day tired, but totally fine. I was able to buy the things I needed, and enjoy time with my sister. The difference was like night and day. For me, a wheelchair is a vital medical aid, not something I’m in for fun.
But, even if I WAS, for some strange reason, using a wheelchair just for fun – why is that any of your business? Are you the wheelchair police? Why should I have to share with you, a complete stranger, my personal medical details, to allow you to decide whether I’m justified in using a wheelchair (or a walking stick, or any other visible medical aid)?
I said at the start that I haven’t used the wheelchair much since we got it. The main reason is because, when I’m sick enough to need the wheelchair, I’m also usually too sick to deal with all the staring and questions from people.
Yes, I’m young to be in a wheelchair.
No, I haven’t ‘done’ anything to myself.
Yes, I have multiple chronic illnesses.
No, it’s not ‘nice’ to have someone push me around (I’d much rather be healthy & walk).
And on… and on…
I know that a lot of people with chronic illnesses don’t use medical aids like walking sticks and wheelchairs in public, because they’re so often interrogated, or even verbally abused for using them. And that makes me sad. If someone spends their days struggling with chronic illness, and they find something that helps them, why should they have to hide it? Because society ‘can’t deal’ with things that don’t fit into their narrow view of disability, many people just miss out, rather than put up with the abuse.
So I’m mad at BuzzFeed. Here was an opportunity for them to correct the misconception that impacts so many people with chronic illness. Here was a chance for them to educate people, and make life easier for those who need medical aids in public.
Instead, they joined in the mocking.
And when Michelle over at Living with Bob called them out on it in this post, I agreed with every word. Here’s an excerpt:
“This is not about a lack of sense of humour, as is often the accusation made when people like myself question such ‘jokes’. Many of us in the chronic illness and disability community have well developed senses of humour. It is what helps make our lives bearable. We find the funny in the most unfunny of experiences. But we are using our own experiences, we mock ourselves not other people. We tread the hard path, the pain, the fear, the tears and the doubt, and we have the right to use our experiences. Others do not.”
Thankfully, when people pointed this out to BuzzFeed in numerous written complaints, BuzzFeed apologised, removed the offensive post, and featured something to correct the misconception they had just perpetuated.
Wait… no.
Sorry, I was dreaming for a moment.
When people complained to BuzzFeed about their insulting post, BuzzFeed pasted several complaints from the disability community into the piece, under the subheading, Disability advocates are offended by coverage of this moment as a “miracle”, and changed the title of the post to Disability Advocates Aren’t Happy That A Man Standing Up From His Wheelchair At The Australian Open Was Called A “Miracle”.
Basically they changed an already insulting post to also make the disability community sound like a bunch of whingers. But that seemed to be their idea of “fixing” the post, because they then added a lovely tag to the end of the piece: “This story has been updated to include comment from disability advocates and to reflect BuzzFeed’s editorial standards for reporting on disability.”
Well, BuzzFeed, thanks for the link!
I read those editorial standards. Obviously you haven’t, because the post you’ve published certainly does not reflect them.
Here’s the “Guidelines for Reporting and Writing about People with Disabilities” you reference. Their dot points include:
* Avoid sensationalizing and negative labeling.
* Emphasize abilities, not limitations.
* Maintain the integrity of each individual.
And the National Center on Disability and Journalism’s style guide that you mentioned?
Here’s their section on people who use wheelchairs, or are wheelchair-bound/confined to a wheelchair.
Background: People who use mobility equipment such as a wheelchair, scooter or cane consider their equipment part of their personal space, according to the United Spinal Association. People who use wheelchairs have widely different disabilities and varying abilities.
NCDJ Recommendation: It is acceptable to describe a person as “someone who uses a wheelchair,” followed by an explanation of why the equipment is required. Avoid “confined to a wheelchair” or “wheelchair-bound” as these terms describe a person only in relationship to a piece of equipment. The terms also are misleading, as wheelchairs can liberate people, allowing them to move about, and they are inaccurate, as people who use wheelchairs are not permanently confined in them, but transfer to sleep, sit in chairs, drive cars, etc.
So, BuzzFeed.
I see you have a cute bar graph at the bottom of your piece, asking for ‘my reaction’ to your post.
Since ‘epic fail’ isn’t an available option, I guess I’ll just have to go with the regular kind.
I think post is a fail on your part, BuzzFeed.
In the words of Gordon Ramsay…

Please use your influence to help the disabled community, instead of mocking us.
We’ve got enough to deal with as it is.
xx S.
If you’d like to read some other bloggers’ posts on this issue, you can click here to read Michelle’s full post about the BuzzFeed piece, or here to read another of her Living with Bob posts about this issue. Or you can click here to read what Sam over at Gimpled has to say.
What do you think of BuzzFeed’s post?
Do you use a wheelchair, walking stick, or other visible medical aid?
Footnotes:
¹ Kaye, H. S., Kang, T. and LaPlante, M.P. (2000). Mobility Device Use in the United States. Disability Statistics Report, (14). Washington, D.C.: U.S. Department of Education, National Institute on Disability and Rehabilitation Research.
Researchers interviewed 1,599 wheelchair users in America. All were non-institutionalised (i.e. not in a nursing home, prison, or a residential facility for mental or physical disabilities). They were just the regular people that you might bump into on the street.
The researchers questioned these wheelchair users on their ability to perform eight tasks, which they called “functional limitations”.
The results show that, while wheelchair users are often limited in many day-to-day areas, they’re not ALL limited in EVERY area. So don’t be surprised when someone using a wheelchair can still do some things, like stand up, walk for a bit, lift an object, or climb some stairs (they might find it difficult – but remember that’s not something you can always see).


Great blog. I’m getting closer and closer to needing a wheelchair, and am already using a cane most days. But I am appalled by the behavior of strangers when they see me with my cane. I have been verbally abused several times on the bus for using a cane at my age and even for just sitting in the disability seats when I don’t have it with me. I can’t imagine how hard it will be once I start using a chair.
LikeLiked by 1 person
Sending hugs xx
I’m sorry that you get this too.
I’ve been verbally abused and physically threatened for using disabled parking (despite always having my permit clearly displayed) since I’m not in a wheelchair, so not ‘obviously’ disabled.
People always tell me looking very young for my age is a blessing, but some days, I can’t wait to look 85! Who’s going to abuse a wrinkly old lady for sitting in a disabled seat, or using a disabled park?
LikeLiked by 1 person
I can relate. Someone once took me to task for walking “too fast” for someone using a cane.
Say what? Gee, I didn’t realize we had a speed limit!
LikeLiked by 2 people
My goodness! Walking too fast?! The things that people feel the need to police never fails to amaze me!
*sigh*
LikeLike
I have Dysautonomia/POTS and joint hyper mobility. My wheelchair is named Freedom and I have been invited to compete in both Miss Wheelchair Florida 2016 and Miss Wheelchair USA. I plan to spread awareness about this very thing!
LikeLiked by 2 people
I’m sorry that you have the POTS / Hypermobility combo too 😦
But I’m thrilled to hear about your plans to use it to raise awareness!
xx S.
LikeLike
Great post! Will share with everyone on my social networks today! I’ve been writing similar lately about the need to get a wheelchair but I can tell actually getting the chair is only half the battle. I anticipate I won’t get much use from it because of fear x
http://cripplebaby.blogspot.ie/2016/02/my-elephant-in-room-wheelchair-conundrum.html?m=0
LikeLiked by 1 person
Thanks for sharing! Maybe if we share enough on this topic, people will start getting it into their thick heads!
Thanks for the link, I just popped over to your blog to read your wheelchair post. It’s a gem! I particularly like the quote about the wheelchair… “If your Mumma didn’t pump out a wheelchair when you were born… you’re a faker”.
I’m sure my Mumma is extremely grateful that is not what happens in real life. Pumping out a baby is difficult enough. Pumping out a wheelchair?! Caesareans all round!
LikeLiked by 1 person
@kittypotpie85, get your chair, if you haven’t already. You’ll get used to people’s rude comments – and once you see how much easier it will make your life, you won’t even care quite as much. At least that’s been my experience since getting mine last year.
The hardest is the first few times, and the first times out around people who are used to seeing you on your feet.
I’ve found that explaining to people what freedom it is giving me convinces most, though, and now my friends just treat it like it’s a normal part of me and the considerations involved in going places.
Actually, truth be told, it’s almost a year now, and I still have times when I feel guilty for using it, but that’s abating. The new thing I have to beat myself up about is the wheelchair van I finally bought a couple of months ago, but FFS, I honestly couldn’t even *get* to a lot of the places I wanted to go and have the chair for otherwise.
When I feel most guilty, I remind myself that a damn good doctor and PT agreed I should have the thing (a power chair in my case, instead of the scooter I’d been expecting to get), and so did my insurance company, which cheerfully paid for it in full, immediately, without question.
LikeLiked by 1 person
ugh! This is my nightmare. I finally am coming to peace with what I just can’t do… but a wheelchair renews some freedoms like, going to an art museum and actually ENJOYING one for the first time in my life? But all that negativity is the reason I get super stressed at the idea. (HyperPOTS and Vasovagal syncope. Standing and me plus the visual stimulation of the museum = bad mojo.) I have a super sweet girlfriend, or an amazing husband, who say they’d go with me and pull the wheelchair around. ❤ My husband says my biggest issue is coming to peace with it fully, so if I did get questioned, I wouldn't be flummoxed on what to say. I think he's right.
LikeLiked by 2 people
That’s what frustrates me the most! That something like a wheelchair, which can give independence and freedom and enjoyment back to people, has so much negativity surrounding it.
I think your husband is very wise. If I start using my wheelchair more frequently, I plan on printing out some little cards with a short explanation of my illness on one side, and the many illnesses wheelchairs are used for on the other side, to help dispel some of the misconceptions. That way, when people question me, I can just hand them one of those cards and move on, without the incident having spoiled my time out.
Would you be interested in some of those? I could pop them up here on my site once I’ve made them, and you could just print them out at home, so that you’re armed for your next excursion? 🙂
❤
LikeLike
Bloody brilliant, I’m not (currently) a stick or chair user but also have EDS and pots, (and chiari) this attitude scares the bejesus out of me TBH, hoping I never need to go through this and I’m beyond sorry on behalf of my fellow humans for their ignorance. As you say we go through enough without conforming, something has to change!
Anyway I just wrote this and thought you / your readers may appreciate.
[Edit: links removed as they didn’t work]
LikeLiked by 1 person
Thanks for the encouragement! We definitely go through enough already. I don’t think my tiny voice will make a huge difference, but even one person helped is better than none!
I removed the links in your comment because they didn’t work 😦 It might just be my settings – I’ll have to check them. In the meantime, can you email me the links for me to check out?
xx S.
LikeLiked by 1 person
https://www.facebook.com/groups/Poemsbyvictoriapayne/permalink/1672180613064298/
Does that work?
It was this poem and my FB site. https://m.facebook.com/groups/Poemsbyvictoriapayne/
Assume you are on FB?
LikeLiked by 1 person
Yep, those ones work! I’ll check them out now 🙂
LikeLike
*claps*
Love them! You’re very talented 🙂
LikeLike
Thank you shared a very thoughtful and encouraging message, after reading this few misconceptions
get actually clear.
LikeLiked by 1 person